在一个线性空间内确定两个线性无关向量,作为基底,它们进行线性组合后扫过的空间就是格。
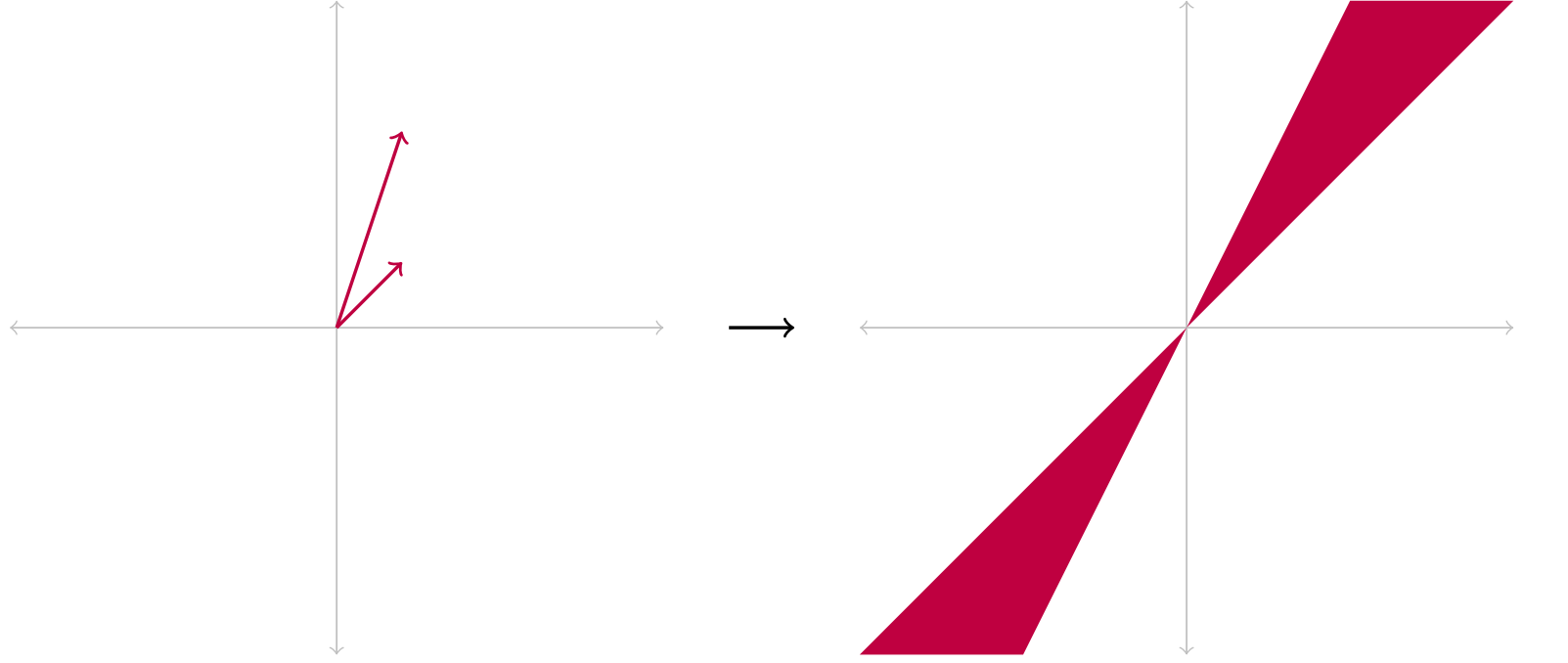 image-20230703205526008
image-20230703205526008在格密码中,我们一般设置基底前的系数为整数,因此形成的格都是离散的。
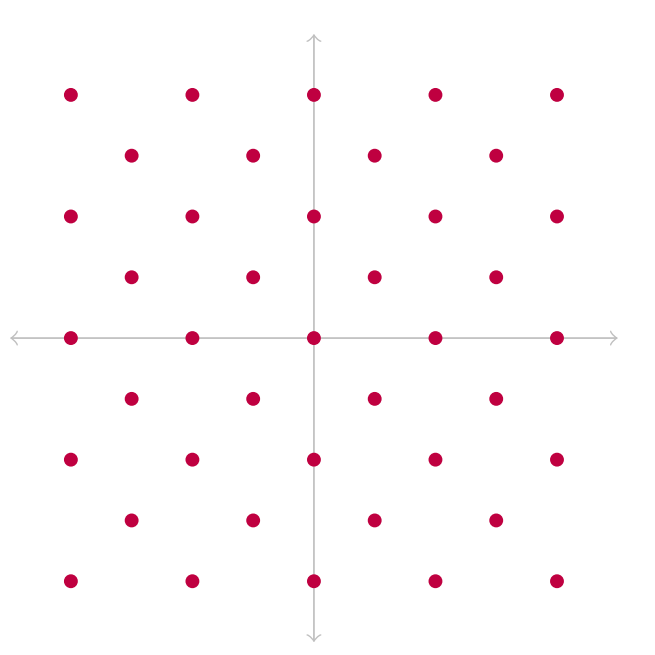 image-20230703205601877
image-20230703205601877格在密码学中很有趣因为我们很少处理实数,而它们给我们提供了很多处理整数的工具。
就像向量空间一样,格也可以用不同的基表示为矩阵来描述。不过与矩阵表示习惯不同的是,我们在格理论中常把基向量作为矩阵的行向量。
下面定义一个格 L{b1,b2,…bω}的行列式:
det(L):=i=1∏ω∣∣bi∣∣
(其实就是矩阵的行列式)
Lenstra-Lenstra-Lov´asz格基约简算法是一种一步一步的演算,可以在多项式时间内减少格基。晶格保持不变,但根据某些定义,其新基的行向量“更小”
Definition 1:设 L 是一个基 B 的格,在 L 的基 B 上应用 LLL 算法产生了 L 的一个新基:B′={b1,…,bn}满足以下条件:
∀1≤j<i≤n 有 ∣μij∣≤21∀1≤i<n 有 δ⋅∣∣bi∣∣2≤∣∣μi+1,i⋅bi+bi+1∣∣同时 μi,j=bj⋅bjbi⋅bj 且 b1=b1(正交化)
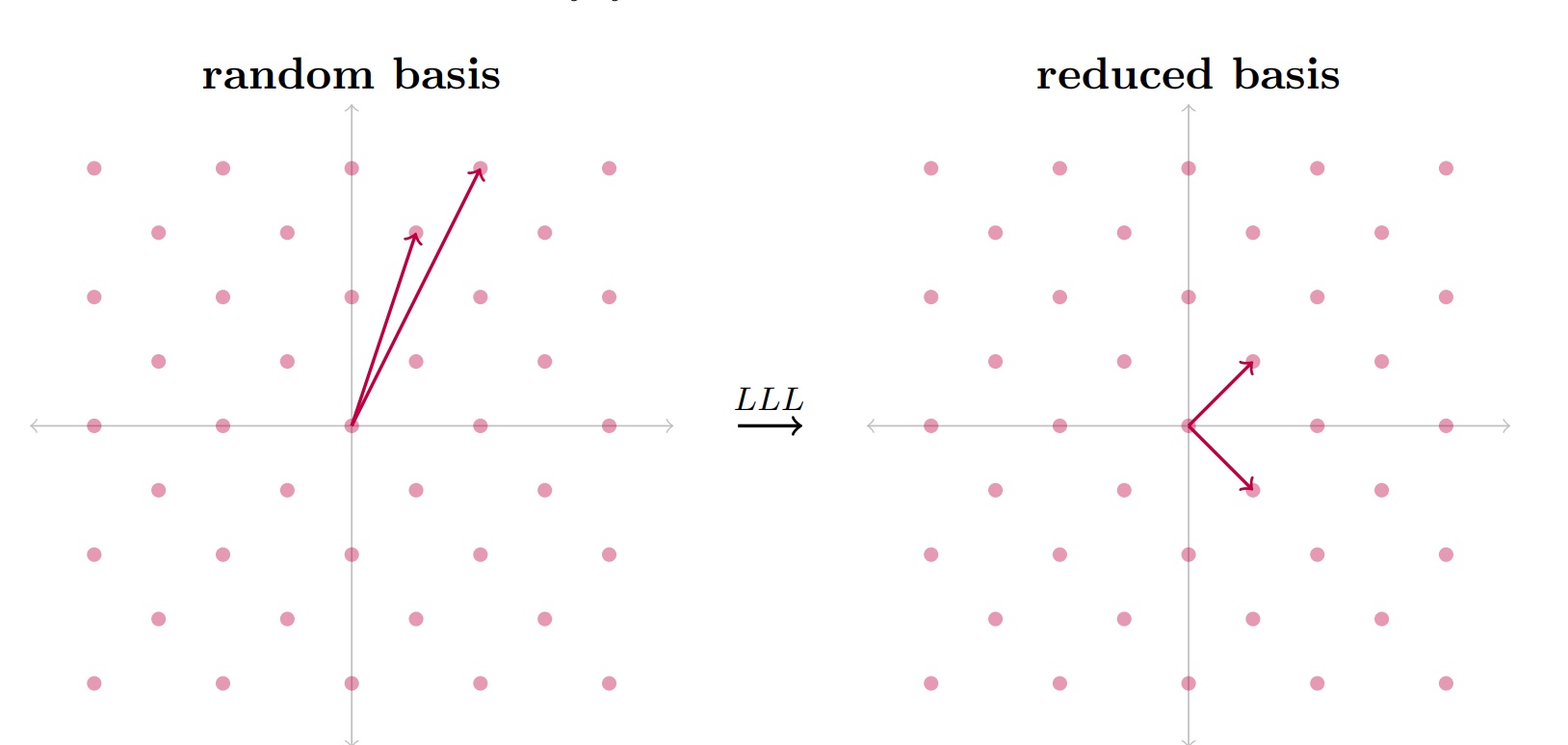 image-20230703211709280
image-20230703211709280LLL 给出了最短向量问题的近似解。这对我们很有用,因为如果我们把晶格基的行向量看作多项式的系数向量。我们可以找到系数“特别小”的多项式的线性组合。
设 L 是一个维数为 n 的格。在多项式时间内,LLL 算法输出约简基向量vi,对于1≤i≤n,满足:
∣∣v1∣∣≤∣∣v2∣∣≤⋯≤∣∣vi∣∣≤24(n+1−i)n(n−1)⋅det(L)n+1−i1
由此,我们可以通过修改格基的维数和行列式来修改向量的界。



